二维数组地址

一、思考

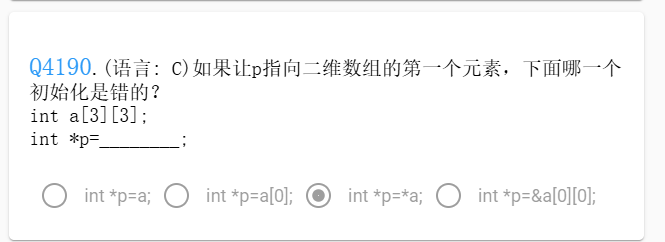
答案：a

二、二维数组地址的表示方法

假设我们定义了一个二维数组：

int a[3][4]; 
// 3行4列，系统分配了 3*4=12 个连续的整数空间

第一层：行地址 (a)

• 含义：a 被视为一个行指针。它指向二维数组的第0行（即把一整行看作一个单位）。
• 类型：int (*)[4] (指向包含4个整数的数组的指针)。
• 步长（+1的效果）：如果你执行 a + 1，地址会跳过整整一行（跳过 4 个 int，即 16 字节），直接指向第1行的起始位置。

第二层：列地址/首元素地址 (a[0] 或 *a)

• 含义：a[0] 代表第0行的一维数组名。数组名代表首元素地址。所以它指向第0行第0个元素。
• 类型：int * (指向单个整数的指针)。
• 步长（+1的效果）：如果你执行 a[0] + 1，地址只会跳过一个元素（跳过 1 个 int，即 4 字节），指向 a[0][1]。
• 理解*a：a表示首行的地址，*a解地址解出来的就是这一行的元素，自然而然就来到的这一行的首地址

有：

int a[3][4];
int b[4];

二维数组中a表示首行的地址，类似一维数组的&b

对二个地址都进行解地址

&b解出来是b，“退化”为数组首元素的地址，a解出来（*a）同理，则是首行的首元素的地址

第三层：具体元素的地址 (&a[0][0])

• 含义：完全等同于 a[0]。
• 类型：int *。

加深理解

在 int a[3][4] 中，以下三个东西打印出来的十六进制地址数值是一模一样的，但它们的“身份”完全不同：

1. a (数组首行地址)
2. a[0] (首行首元素地址)
3. &a[0][0] (首行首元素地址)

打个比方：

• a 就像“第一排座位”的标签。
• a[0] 就像“第一排第一个座位”的标签。
• 虽然它们物理位置都在同一个地方，但如果你说“下一排”(a+1)，你会跨过整排；如果你说“下一个座位”(a[0]+1)，你只跨过一个人。

万能公式图解

如果要访问第 i 行，第 j 列的元素，以下几种表达方式是等价的：

表达方式	含义	类型	备注
a[i][j]	值	int	取值
&a[i][j]	地址	int *	取第i行第j个元素的地址
a[i] + j	地址	int *	第i行首地址向后移j个元素
*(a + i) + j	地址	int *	同上
a + i	地址	int (*)[4]	第i行的首地址 (行指针)